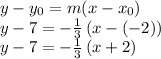Answer:
The point slope form is:
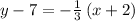
Explanation:
Recall the general point-slope form of a line of slope "m" and going through a point
 , is given by:
, is given by:

Notice therefore, that the given line is expressed in "point-slope" form
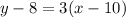
where the slope is given by the value: "3".
Recall that the slope of a line perpendicular to another given line of known slope "m" is the "opposite of the reciprocal" of that "m". That is:
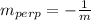
Then for our case, the line perpendicular to the one given, must have slope given by:
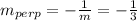
So now we can create easily the point-slope form of the requested perpendicular line that goes through the point (-2,7) using the general point-slope form mentioned above: