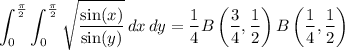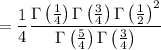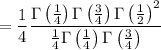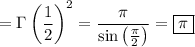Question

Evaluate this:


`\displaystyle\rm\int_0^(\pi)/(2)√(\sin x)\ dx * \int_0^(\pi)/(2)(1)/(√(\sin x))\ dx`

Only elementary methods are allowed.​

Answer 1

The first integral has a well-known beta function representation, so the second one should too. The beta function itself is defined as

`B(x,y) = \displaystyle \int_0^1 t^(x-1) (1-t)^(y-1) \, dt`

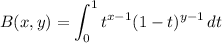
and satisfies the identity

`\displaystyle B(x,y) = (\Gamma(x) \Gamma(y))/(\Gamma(x+y))`

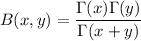
Later on, we'll also use the so-called reflection formula for the gamma function; for non-integer z,

`\Gamma(z) \Gamma(1-z) = (\pi)/(\sin(\pi z))`

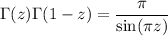
as well as the identity

`(\Gamma(z+1))/(\Gamma(z)) = z`

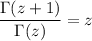
Replace
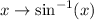`x\to\sin^(-1)(x)` in both integrals, so that

`\displaystyle \int_0^(\frac\pi2) √(\sin(x)) \, dx = \int_0^1 (\sqrt x)/(√(1-x^2)) \, dx`

`\displaystyle \int_0^(\frac\pi2) (dx)/(√(\sin(x))) = \int_0^1 (dx)/(\sqrt x √(1-x^2))`

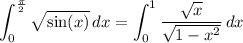
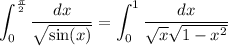
Now replace
`x\to\sqrt x` :

`\displaystyle \int_0^1 (\sqrt x)/(√(1-x^2)) \, dx = \frac12 \int_0^1 x^(-\frac14) (1-x)^(-\frac12) \, dx = \frac12 B\left(\frac34, \frac12\right)`

`\displaystyle \int_0^1 (dx)/(\sqrt x √(1-x^2)) = \frac12 \int_0^1 x^(-\frac34) (1-x)^(-\frac12) \, dx = \frac12 B\left(\frac14, \frac12\right)`

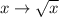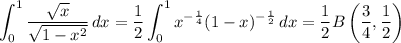
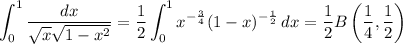
So, the original integral (which I condense here to a double integral) is

`\displaystyle \int_0^(\frac\pi2) \int_0^(\frac\pi2) \sqrt{(\sin(x))/(\sin(y))} \, dx \, dy = \frac14 B\left(\frac34, \frac12\right) B\left(\frac14, \frac12\right)`

`\displaystyle = \frac14 (\Gamma\left(\frac14\right) \Gamma\left(\frac34\right) \Gamma\left(\frac12\right)^2)/(\Gamma\left(\frac54\right) \Gamma\left(\frac34\right))`

`\displaystyle = \frac14 (\Gamma\left(\frac14\right) \Gamma\left(\frac34\right) \Gamma\left(\frac12\right)^2)/(\frac14 \Gamma\left(\frac14\right) \Gamma\left(\frac34\right))`

`\displaystyle = \Gamma\left(\frac12\right)^2 = (\pi)/(\sin\left(\frac\pi2\right)) = \boxed{\pi}`