Answer:
Yes;
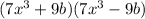
Explanation:
A difference of squares is basically where you have two terms that can both be written in the form of
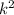 and one is subtracting the other.
and one is subtracting the other.
Here, the first term is
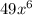 . We see that if we square root this, we will come out with the clean number:
. We see that if we square root this, we will come out with the clean number:
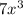 (because
(because
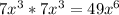 ).
).
The second term is
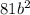 . Again, we see that if we square root this, we will get the clean result:
. Again, we see that if we square root this, we will get the clean result:
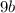 (because
(because
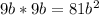 ).
).
So, they are indeed both squares; thus, this is a difference of squares.
To factor it, we remember the formula for factoring
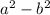 :
:
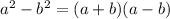
In this case, a = 7x^3 and b = 9b, so:
 , and that's the answer.
, and that's the answer.
Hope that helps!