The equivalent equations to the trapezoid area formula
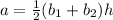 are
are
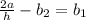 and
and
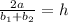 , expressing the relationship between area, height, and base lengths.
, expressing the relationship between area, height, and base lengths.
The trapezoid area formula
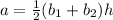 describes the area a in terms of height h, and base lengths
describes the area a in terms of height h, and base lengths
 . The equivalent equations are:
. The equivalent equations are:
a.
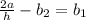 - Represents a valid rearrangement of the formula.
- Represents a valid rearrangement of the formula.
d.
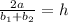 - Expresses height h in terms of area
- Expresses height h in terms of area
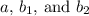 .
.
These equations are equivalent to the given trapezoid area formula, providing alternate ways to express the relationship between area, height, and base lengths.