Question

An airplane is flying in a direction of 75 degrees north of east at a constant flight speed of 300 miles per hour. Th wind is blowing due west at a speed of 25 miles per hour. What is the actual direction of the airplane? Round your answer to the nearest tenth. Show your work

Answer 1

The resultant speed is 294.5 mi/h in a direction N79.7°E

Explanation:

Let

East and North as the positive x and y-axis, respectively.

West and South as the negative x- and y-axis, respectively.

step 1

Take the x- and y-components of the speeds.

Airplane:

`x-component = (300\ mi/hr)cos(75^o)= 77.6\ mi/h`

`y-component = (300\ mi/hr)sin(75^o)= 289.8\ mi/h`

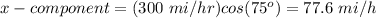
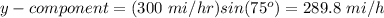
Wind:

`x-component = -25\ mi/hr`

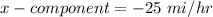
step 2

Adding up the components:

`x-component =77.6-25= 52.6\ mi/hr`

`y-component = 289.8\ mi/hr`

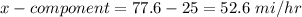
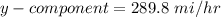
step 3

Find the resultant speed

`R = √((Rx)^2 + (Ry)^2)`

`R = √((52,6)^2 + (289.8)^2)`

`R=294.5\ mi/h`

step 4

Find the direction

`tan(\theta)=(Ry)/(Rx)`

substitute

`tan(\theta)=(289.8)/(52.6)`

`\theta=tan^(-1)((289.8)/(52.6))=79.7^o`

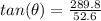
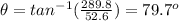
therefore

The resultant speed is 294.5 mi/h in a direction N79.7°E