Question

The owner of an orange grove must decide when to pick one variety of oranges. She can sell them for $27 a bushel if she sells them now, with each tree yielding an average of 7 bushels. The yield increases by half a bushel per week for the next 5 weeks, but the price per bushel decreases by $1.50 per bushel each week. In how many weeks should the oranges be picked for maximum return?

Answer 1

The oranges should be picked in 2 weeks for maximum return

Step-by-step explanation:

We assume that the return of the owner is y ($)

Assume that the number of weeks the oranges should be picked to have maximum return is x (weeks). (x≥0)

If collect now, the price for each bushel is $27

As the price per bushel decrease by $1.50 per bushel each week

=> After x weeks, the price of a bushel decrease: 1.5x ($)

=> The price of 1 bushel after x weeks is: 27 - 1.5x ($)

If collect now, each tree can yield 7 bushels

As the yield increases by half a bushel per week for the next 5 weeks

=> After x weeks with x ≤ 5, each trees would yields: 7 + 0.5x (bushels)

The return = The price of each bushes × The quantity of bushels

=>
`y = (27-1.5x)(7+0.5x)`

⇔
`y= 27 (7 +0.5x) - 1.5x(7+0.5x) = 189 + 13.5x - 10.5x - 0.75x^(2)`

⇔
`y = -0.75x^(2) +3x +189`

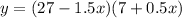
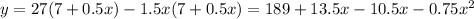
We have: if the equation has the form of
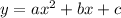`y =ax^(2) +bx +c` with a≠0, its maximum value is:
`max y = c - (b^(2) )/(4a)`

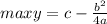
In the equation
`y = -0.75x^(2) +3x +189`, we have: a = -0.75; b = 3; c = 189

=>
`max y = c -(b^(2) )/(4a) = 189 - (3^(2) )/(4.(-0.75)) = 189 - (9)/(-3) = 189 - (-3) = 189+3 = 192`

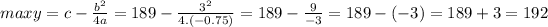
To look for the number of weeks, we should find x (0≤x≤5) with which y = 192

`192 = -0.75x^(2) +3x +189`

⇔
`-0.75x^(2) + 3x + 189 - 192 = 0`

⇔
`-0.75 x^(2) + 3x - 3 =0`

⇔
`-0.75x^(2) + 4*0.75x - 0.75*4 =0`

⇔
`x^(2) -4x + 4 = 0`

⇔
`(x-2)^(2) = 0`

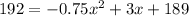
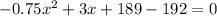
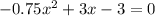
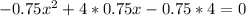
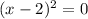
⇔ x = 2

The oranges should be picked in 2 weeks for maximum return