1 Answer

Shandell · Answer 1 · 2021-05-14T09:52:47+0000

The distance between point F and point G is option 1. 4.5 units.

Explanation:

Step 1:

First, we plot the points F and G.

The point F is at (-1, 6) and point G is at (3, 4).

To calculate the distance between these two points, we use the formula

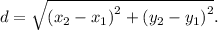
$d=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}.$

Step 2:

Take point F as the first point and point G as the second point.

So
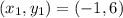(x_(1), y_(1)) = (-1, 6) and
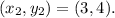
(x_(2), y_(2)) = (3, 4).

Substituting the values in the equation, we get

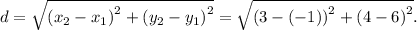
$d=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)} =√(\left(3-(-1))\right)^(2)+\left(4-6\right)^(2)}.$

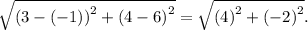
$√(\left(3-(-1))\right)^(2)+\left(4-6\right)^(2)} = √(\left(4)\right)^(2)+\left(-2\right)^(2)}.$

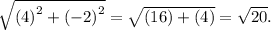
$√(\left(4)\right)^(2)+\left(-2\right)^(2)} = √(\left(16)\right)+\left(4\right)} = √(20) .$

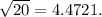
√(20) = 4.4721.

Rounding this off, we get that the distance between point F and point G is 4.5 units.

Please log in or register to add a comment.