The coordinates are A(-5,3), B(7,1) and C(-3,-1).
Explanation:
Given,
The midpoints of the sides AB, BC and AC are (1,4) , (2,0) and (-4,1) respectively.
To find the coordinates of A, B, C.
Let,
The coordinates of A,B and C are (a,x), (b,y) and (c,z) respectively.
Formula
The mid point of two given points (
 ) and (
) and (
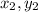 ) is (
) is (
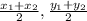 )
)
Now,
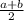 = 1 and
= 1 and
 = 4 ⇒ a+b = 2 ---(1) and x+y = 4 --(2)
= 4 ⇒ a+b = 2 ---(1) and x+y = 4 --(2)
 = 2 and
= 2 and
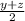 = 0 ⇒ b+c = 4 ---(3) and y+z = 0---(4)
= 0 ⇒ b+c = 4 ---(3) and y+z = 0---(4)
 = -4 and
= -4 and
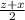 = 1 ⇒ c+a = -8 ---(5) and z+x = 2 ----(6)
= 1 ⇒ c+a = -8 ---(5) and z+x = 2 ----(6)
Adding (1), (3) and (5) we get,
2(a+b+c) = -2
or, a+b+c = -1
So, a = -5, b = 7 and c = -3
Similarly Adding (2), (4) and (6) we get,
2(x+y+z) = 6
or, x+y+z = 3
So, x = 3, y = 1 and z = -1
Hence,
The coordinates are A(-5,3), B(7,1) and C(-3,-1).