Question

Assume that when you stretch your torso vertically as much as you can, your center of mass is 1.0 m above the floor. The maximum force you can exert on the floor in pushing off is 2.3 times the gravitational force Earth exerts on you

How low do you have to crouch in order to jump straight up and have your center of mass be 2.0 m above the floor? Determine the lowest height of your center of mass above the floor in the jump.?

Is this crouch practical?

Answer 1

1) 0.77 m

2) 0.23 m

Step-by-step explanation:

1)

Here we want to find the time elapsed for crouching in order to jump and reach a height of 2.0 m above the floor, starting from 1.0 m above the floor.

First of all, we start by calculating the speed required to jump up to a height of 2.0 m. Since the total energy is conserved, the initial kinetic energy is converted into gravitational potential energy, so:

`(1)/(2)mv^2 = mgh`

where

m is the mass of the man

v is the speed after jumping

`g=9.8 m/s^2` is the acceleration due to gravity

h = 2.0 - 1.0 = 1.0 m is the change in height

Solving for v,

`v=√(2gh)=√(2(9.8)(1.0))=4.43 m/s`

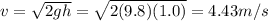
In the acceleration phase, we know that the initial velocity is

`u=0`

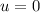
And the force exerted on the floor is 2.3 times the gravitational force, so

`F=2.3 mg`

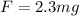
This means the net force on you is

`F_(net) = F-mg=2.3mg-mg=1.3 mg`

because we have to consider the force of gravity acting downward.

So the acceleration of the man is

`a=(F_(net))/(m)=(1.3mg)/(m)=1.3g`

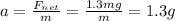
Now we can use the following suvat equation to find the displacement in the acceleration phase, which is how low the man has to crouch in order to jump:

`v^2-u^2=2as`

where s is the quantity we want to find. Solving for s,

`s=(v^2-u^2)/(2a)=(4.43^2-0)/(2(1.3g))=0.77 m`

2)

At the beginning, we are told that the height of the center of mass above the floor is

h = 1.0 m

During the acceleration phase and the crouch, the height of the center of mass of the body decreases by

`\Delta h = -0.77 m`

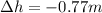
This means that the lowest point reached by the center of mass above the floor during the crouch is

`h'=h+\Delta h = 1.0 - 0.77 = 0.23 m`

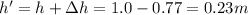
This value seems unpractical, since it is not really easy to crouch until having the center of mass 0.23 m above the ground.