Question

Find Area to the nearest tenth

Answer 1

The area of the square is 288 square units.

Explanation:

Step 1:

The triangle has a hypotenuse measuring 12 units.

According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Since the triangle intersects with the center of the square, the other two sides are equal in length.

Assume x is the length of both the unknown sides.

So
`12^(2) = x^(2) +x^(2) = 2x^(2) .`

`2x^(2) = 144, x^(2) = 72.`

`x = √(72) = 8.4852.`

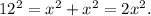
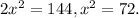
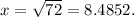
x is only half the side length of the square so the side length of the square is
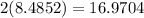`2(8.4852) = 16.9704` units. So the side length of the square is 16.9704 units.

Step 2:

The area of a square is the square of the side length.

The area of the square
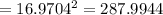`= 16.9704^(2) = 287.9944` square units.

Rounding this off, we get that the area of the square is 288 square units.