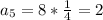Question

5) Find the common ratio and the next term.
512, 128, 32, 8,

Answer 1

The common ratio is
`(1)/(4)`

The next term in the sequence is 2

Explanation:

In a geometric sequence, the common ratio is the constant value you multiply a term by in order to find the value of the following term. Therefore, it is mathematically calculated as the quotient between a term and the term immediately before it. And it is in fact That is:

common ratio
`r=(a_(n+1))/(a_n)`

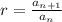
This quotient should be true for any two consecutive terms in the sequence.

so using the first two terms, we find:

`r=(a_(n+1))/(a_n)=(a_(2))/(a1)=(128)/(512) =(1)/(4)`

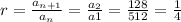
You can test that this common ratio is true for all other terms listed:

`(a_3)/(a_2) =(32)/(128) =(1)/(4) \\(a_4)/(a_3) =(8)/(32) =(1)/(4) \\`

So now, in order to find the term that follows, all we need to do is to multiply the last term given (8) by this common ratio:

`a_5=8*(1)/(4) =2`