Answer :

Explanation :
- This is Right Angled Trian1gle.

Solution :
- We'll solve this using the Pythagorean Theorem.

Where,
- VW (9 mm) is the Hypotenuse.
- UW is the Perpendicular .

We know that,
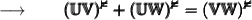
Now, we will substitute the given values in the formula :
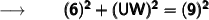
We know that, (6)² = 36 and (9)² = 81. So,
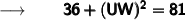
Now, transposing 36 to the other side we get :
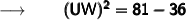
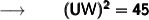
Now, we'll take the square root of both sides to remove the square from UW :
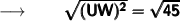
When we take the square root of (UW)² , it becomes UW,

We know that, square root of 45 is 6.708.
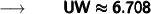
So,
- The measure of the missing side (UW) is 6.7 mm (Rounded to nearest tenth)