Given:
From the figure, the sides are (2x + 5), (x + 12), (y - 4) and (x + 5)
The sides having lengths (2x + 5) and (x + 12) are equal.
The sides having lengths (y - 4) and (x + 5) are equal.
We need to solve the given figure.
Value of x:
Let us determine the value of x.
Equating the two sides having equal lengths (2x + 5) and (x + 12), we get;
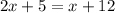
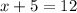
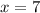
Thus, the value of x is 7.
Value of y:
The value of y can be determined by equating the two sides (y - 4) and (x + 5) having equal lengths.
Thus, we have;
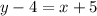
Substituting x = 7, we get;
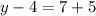
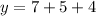

Thus, the value of y is 16.
Side lengths of the figure:
The side lengths can be determined by substituting the values of x and y.
Thus, we have;
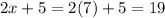
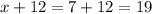
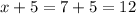
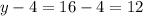
Thus, the lengths of the figure are 19, 19, 12, 12.