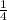Question

An equation shows m is directly proportional to n and inversely proportional to

s cubed. When m = 5, then n = 160 and s = 2. What is the constant of
proportionality? Write your answer as a fraction.

Answer 1

Given:

An equation shows m is directly proportional to n and inversely proportional to s cubed.

This can be written in expression as,

`m=k(n)((1)/(s^3))`

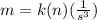
We need to determine the constant of proportionality when m = 5, n = 160 and s = 2.

Constant of proportionality:

The constant of proportionality can be determined by substituting m = 5, n = 160 and s = 2 in the equation
`m=k(n)((1)/(s^3))`

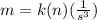
Thus, we have;

`5=k(160)((1)/(2^3))`

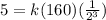
Simplifying, we get;

`5=k(160)((1)/(8))`

`5=20k`

`(5)/(20)=k`

`(1)/(4)=k`

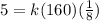
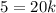
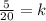
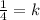
Thus, the value of the constant of proportionality is
`(1)/(4)`