Question

According to a marketing research study, American teenagers watched 16.5 hours of social media posts per month last year, on average. A random sample of 20 American teenagers was surveyed and the mean amount of time per month each teenager watched social media posts was 17.3. This data has a sample standard deviation of 2.1. (Assume that the scores are normally distributed.) Researchers conduct a one-mean hypothesis at the 10% significance level to test if the mean amount of time American teenagers watch social media posts per month is greater than the mean amount of time last year. Which answer choice shows the correct null and alternative hypotheses for this test? Select the correct answer below: H0:μ=17.3; Ha:μ<17.3, which is a left-tailed test. H0:μ=17.3; Ha:μ>17.3, which is a right-tailed test. H0:μ=16.5; Ha:μ<16.5, which is a left-tailed test. H0:μ=16.5; Ha:μ>16.5, which is a right-tailed test.

Answer 1

Null Hypothesis:
`\mu \geq 16.5`

Alternative hypothesis:
`\mu <16.5`

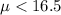
And the correct option for this case would be:

H0:μ=16.5; Ha:μ<16.5, which is a left-tailed test

And the data for this case we have this sample data:

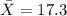`\bar X= 17.3` the sample mean

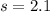`s= 2.1` the sample deviation

n =20 the sample size

Explanation:

Previous concepts

The null hypothesis attempts "to show that no variation exists between variables or that a single variable is no different than its mean"

The alternative hypothesis "is the hypothesis used in hypothesis testing that is contrary to the null hypothesis"

Solution to the problem

For this case we want to test if the mean amount of time American teenagers watch social media posts per month is greater than the mean amount of time last year (alternative hypothesis), and the system of hypothesis are:

Null Hypothesis:
`\mu \geq 16.5`

Alternative hypothesis:
`\mu <16.5`

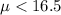
And the correct option for this case would be:

H0:μ=16.5; Ha:μ<16.5, which is a left-tailed test

And the data for this case we have this sample data:

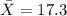`\bar X= 17.3` the sample mean

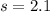`s= 2.1` the sample deviation

n =20 the sample size