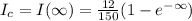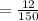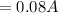Question

What is the current I(3τ), that is, the current after three time constants have passed? The current in the circuit will approach a constant value Ic after a long time (as t tends to infinity). What is Ic?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

`I(\tau)=0.051 A`

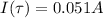
b

`I(3 \tau)=0.076 A`

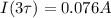
c

`I_c= 0.08 A`

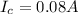
Step-by-step explanation:

From the question we are told that

`I(t) = (e)/(R)(1-e^{(t)/(\tau) }) ; \ Where \ \tau = L/R`

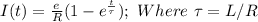
From the question we are told to find
`I(\tau)` when t=0 equals the time constant (
`\tau`)

That is to obtain
`I(\tau)`.This is mathematically represented as

`I(\tau = t) = (\epsilon)/(R) (1- e^{-(\tau)/(\tau) })`

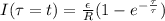
Substituting 12 V for
`\epsilon` and 150Ω for R

`I(\tau) = (12)/(150) (1- e^(-1))`

`=0.051 A`

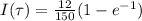
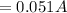
From the question we are told to find
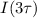`I(3 \tau)` when t=0 equals the 3 times the time constant (
`\tau`)

That is to obtain
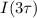`I(3\tau)`.This is mathematically represented as

`I(\tau = t) = (\epsilon)/(R) (1- e^{-(3\tau)/(\tau) })`

`I(\tau) = (12)/(150) (1- e^(-3))`

`=0.076 A`

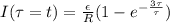
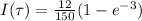
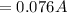
As tends to infinity
`(\infty)/(\tau) = \infty`

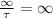
So
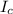`I_c` would be mathematically evaluated as

`I_c=I(\infty) = (12)/(150) (1- e^(- \infty))`

`= (12)/(150)`

`= 0.08 A`