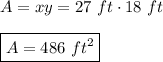Answer:
27 feet for the south wall and 18 feet for the east/west walls
Maximum area=
Explanation:
Optimization
This is a simple case where an objective function must be minimized or maximized, given some restrictions coming in the form of equations.
The first derivative method will be used to find the values of the parameters that control the objective function and the maximum value of that function.
The office space for Billy-Sean will have the form of a rectangle of dimensions x and y, being x the number of feet for the south wall and y the number of feet for the west wall. The total cost of the space is
C=8x+12y
The budget to build the office space is $432, thus
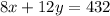
Solving for y

The area of the office space is
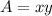
Replacing the value found above
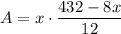
Operating
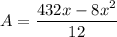
This is the objective function and must be maximized. Taking its first derivative and equating to 0:
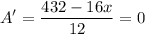
Operating
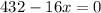
Solving
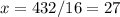
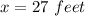
Calculating y
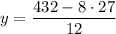
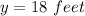
Compute the second derivative to ensure it's a maximum

Since it's negative for x positive, the values found are a maximum for the area of the office space, which area is