Question

Part 4: Use the information provided to write the vertex formula of each parabola.

1. Focus: (-31/4, 2), Directrix: x = -33/4

2. Focus: (1/2, 10), Directrix: x = 3/2

3. Focus: (-9, 57/8), Directrix: y= 55/8

Answer 1

Answer: 1. x = (y - 2)² + 8

`\bold{2.\quad x=-(1)/(2)(y-10)^2}+1`

3. y = 2(x +9)² + 7

Explanation:

Notes: Vertex form is: y =a(x - h)² + k or x =a(y - k)² + h

• (h, k) is the vertex
• point of vertex is midpoint of focus and directrix:
  `(focus+directrix)/(2)`

`\bullet\quad a=(1)/(4p)`

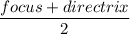
• p is the distance from the vertex to the focus

1)

`focus = \bigg((-31)/(4),2\bigg)\qquad directrix: x=(-33)/(4)\\\\\text{Since directrix is x, then the x-value of the vertex is:}\\\\(focus+directrix)/(2)=((-31)/(4)+(-33)/(4))/(2)=((-64)/(4))/(2)=(-16)/(2)=-8\\\\\text{The y-value of the vertex is given by the focus as: 2}\\\\\text{vertex (h, k)}=(-8,2)`

Now let's find the a-value:

`p=focus-vertex\\\\p=(-31)/(4)-(-32)/(4)=(1)/(4)\\\\\\a=(1)/(4p)=(1)/(4((1)/(4)))=(1)/(1)=1`

Now, plug in a = 1 and (h, k) = (-8, 2) into the equation x =a(y - k)² + h

x = (y - 2)² + 8

***************************************************************************************

2)

`focus = \bigg((1)/(2),10\bigg)\qquad directrix: x=(3)/(2)\\\\\text{Since directrix is x, then the x-value of the vertex is:}\\\\(focus+directrix)/(2)=((1)/(2)+(3)/(2))/(2)=((4)/(2))/(2)=(2)/(2)=1\\\\\text{The y-value of the vertex is given by the focus as: 10}\\\\\text{vertex (h, k)}=(1,10)`

Now let's find the a-value:

`p=focus-vertex\\\\p=(1)/(2)-(2)/(2)=(-1)/(2)\\\\\\a=(1)/(4p)=(1)/(4((-1)/(2)))=(1)/(-2)=-(1)/(2)`

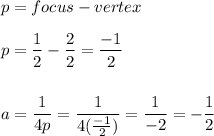
Now, plug in a = -1/2 and (h, k) = (1, 10) into the equation x =a(y - k)² + h

`\bold{x=-(1)/(2)(y-10)^2}+1`

***************************************************************************************

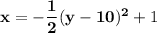
3)

`focus = \bigg(-9,(57)/(8)\bigg)\qquad directrix: y=(55)/(8)\\\\\text{Since directrix is y, then the y-value of the vertex is:}\\\\(focus+directrix)/(2)=((57)/(8)+(55)/(8))/(2)=((112)/(8))/(2)=(14)/(2)=7\\\\\text{The x-value of the vertex is given by the focus as: -9}\\\\\text{vertex (h, k)}=(-9,7)`

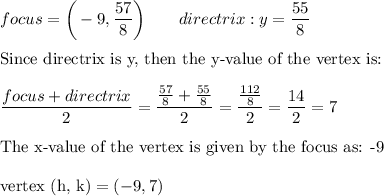
Now let's find the a-value:

`p=focus-vertex\\\\p=(57)/(8)-(56)/(8)=(1)/(8)\\\\\\a=(1)/(4p)=(1)/(4((1)/(8)))=(1)/((1)/(2))=2`

Now, plug in a = 2 and (h, k) = (-9, 7) into the equation y =a(x - h)² + k

y = 2(x +9)² + 7