Given:
The given equation is
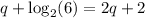
We need to determine the approximate value of q.
Value of q:
To determine the value of q, let us solve the equation for q.
Hence, Subtracting
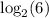 on both sides of the equation, we get;
on both sides of the equation, we get;

Subtracting both sides of the equation by 2q, we have;

Dividing both sides of the equation by -1, we have;
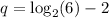
Now, substituting the value of
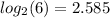 , we have;
, we have;
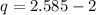
Subtracting the values, we get;
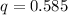
Thus, the approximate value of q is 0.585
Hence, Option C is the correct answer.