Question

Help me please I’m having trouble with it

Answer 1

Given:

Measure of arcs 50°, 115° and 85°

To find:

The measure of the numbered angle 5.

Solution:

Let the missing arc measure be A.

The arc measure of a full circle is 360°

m(ar A) + 50° + 115° + 85° = 360°

m(ar A) + 250° = 360°

Subtract 250 from both sides.

m(ar A) = 110°

If two chords intersects inside a circle, then the measure of the angle formed is half of the sum of intercepted arcs.

`$\Rightarrow m\angle 5 =(1)/(2) (110^\circ+115^\circ)`

`$\Rightarrow m\angle 5 =(1)/(2) (225^\circ)`

`$\Rightarrow m\angle 5 =112.5^\circ`

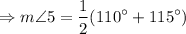
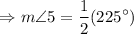
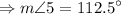
The measure of the numbered angle is 112.5°.