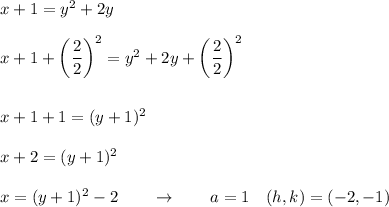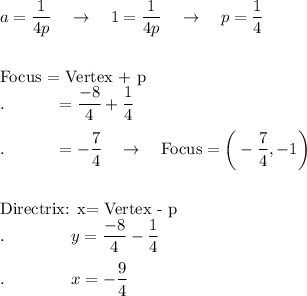Question

Part 4: Identify the vertex, focus and directrix of each. Then sketch the graph.

1. y = x^2 - 12x + 34

2. x = y^2 + 2y - 1

Answer 1

Answer: 1) Vertex: (6, -2) Focus: (6, -7/4) Directrix: y = -9/4

2) Vertex: (-2, -1) Focus: (-7/4, -1) Directrix: x = -9/4

Explanation:

Rewrite the equation in vertex format y = a(x - h)² + k or x = a(y - k)² + h by completing the square. Divide the b-value by 2 and square it - add that value to both sides of the equation.

• (h, k) is the vertex
• p is the distance from the vertex to the focus
• -p is the distance from the vertex to the directrix

`\bullet\quad a=(1)/(4p)`

1) y = x² - 12x + 34

`y-34=x^2-12x\\\\y-34+\bigg((-12)/(2)\bigg)^2=x^2-12x+\bigg((-12)/(2)\bigg)^2\\\\\\y-34+36=(x-6)^2\\\\y+2=(x-6)^2\\\\y=(x-6)^2-2\qquad \rightarrow \qquad a=1\quad (h,k)=(6,-2)\\`

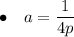
`a=(1)/(4p)\quad \rightarrow \quad 1=(1)/(4p)\quad \rightarrow \quad p=(1)/(4)\\\\\\\text{Focus = Vertex + p}\\.\qquad \quad =(-8)/(4)+(1)/(4)\\\\.\qquad \quad =-(7)/(4)\quad \rightarrow \quad\text{Focus}=\bigg(6,-(7)/(4)\bigg)\\\\\\\text{Directrix: y= Vertex - p}\\.\qquad \qquad y=(-8)/(4)-(1)/(4)\\\\.\qquad \qquad y=-(9)/(4)`

*******************************************************************************************

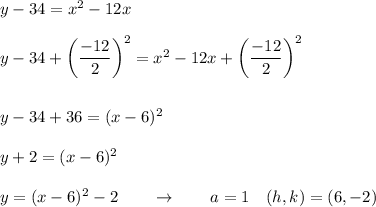
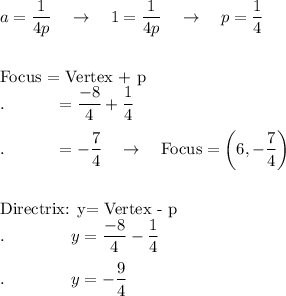
2) x = y² + 2y - 1

`x+1=y^2+2y\\\\x+1+\bigg((2)/(2)\bigg)^2=y^2+2y+\bigg((2)/(2)\bigg)^2\\\\\\x+1+1=(y+1)^2\\\\x+2=(y+1)^2\\\\x=(y+1)^2-2\qquad \rightarrow \qquad a=1\quad (h,k)=(-2,-1)\\`

`a=(1)/(4p)\quad \rightarrow \quad 1=(1)/(4p)\quad \rightarrow \quad p=(1)/(4)\\\\\\\text{Focus = Vertex + p}\\.\qquad \quad =(-8)/(4)+(1)/(4)\\\\.\qquad \quad =-(7)/(4)\quad \rightarrow \quad\text{Focus}=\bigg(-(7)/(4),-1\bigg)\\\\\\\text{Directrix: x= Vertex - p}\\.\qquad \qquad y=(-8)/(4)-(1)/(4)\\\\.\qquad \qquad x=-(9)/(4)`