Answer :
⠀
Explanation :
- This is Right Angled Triangle.
⠀
Solution :
- We'll solve this using the Pythagorean Theorem.
where,
- XY (3 yd) is the perpendicular
We know that,
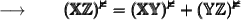
Now, we will substitute the given values in the formula :
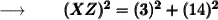
We know that, (3)² = 9 and (14)² = 196. So,
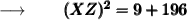
Now, adding 9 and 196 we get :
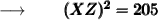
Now, we'll take the square root of both sides to remove the square from XZ :
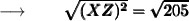
When we take the square root of (XZ)² , it becomes XZ,
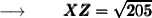
We know that, square root of 205 is 14.317 (approx) .
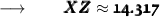
So,
- The measure of the missing side (XZ) is 14.3 (Rounded to nearest tenth)