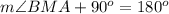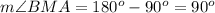Question

Jack is a civil engineer and uses angle relationships to design public structures such as buildings, bridges, and streets. He designs walking paths in a park as shown below.

Rectangle A B C D has diagonals B D and A C that intersect at the center of the rectangle at point M. Angle M A D is 30 degrees and angle M D A is 60 degrees.

What is the measure of angle BMA where the diagonals meet?

°

Answer 1

90

Explanation:

Answer 2

The measure of angle BMA is 90 degrees

Explanation:

The picture of the question in the attached figure

step 1

Find the measure of angle AMD

we know that

The sum of the interior angles in any triangle must be equal to 180 degrees

In the triangle MAD

`m\angle MAD+m\angle MDA+m\angle AMD=180^o`

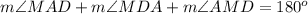
substitute the given values

`30^o+60^o+m\angle AMD=180^o`

`m\angle AMD=180^o-90^o=90^o`

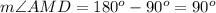
step 2

Find the measure of angle BMA

we know that

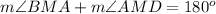`m\angle BMA+m\angle AMD=180^o` ---> by supplementary angles (form a linear pair)

substitute the given value

`m\angle BMA+90^o=180^o`

`m\angle BMA=180^o-90^o=90^o`