Question

A ball is kicked 4 feet above the ground with an initial vertical velocity of 55 feet per second. The function h(t)=−16t2+55t+4 represents the height h (in feet) of the ball after t seconds. Using a graph, after how many seconds is the ball 30 feet above the ground? Round your answers to the nearest tenth.

I would like to know both the answer and the steps to get there please and i need it asap. Thank you!

Answer 1

Given:

A ball is kicked 4 feet above the ground with an initial vertical velocity of 55 feet per second.

The function
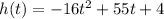`h(t)=-16t^2+55t+4` represents the height h(in feet) of the ball after t seconds.

We need to determine the time of the ball at which it is 30 feet above the ground.

Time:

To determine the time that it takes for the ball to reach a height of 30 feet above the ground, let us substitute h(t) = 30, we get;

`30=-16t^2+55t+4`

`26=-16t^2+55t`

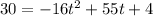
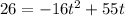
Adding both sides of the equation by 16t², we get;

`16t^2+26=55t`

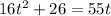
Subtracting both sides of the equation by 55t, we have;

`16t^2-55t+26=0`

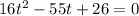
Let us solve the quadratic equation using the quadratic formula, we get;

`t=(-(-55) \pm √((-55)^2-4(16)(26)))/(2(16))`

`t=(55 \pm √(3025-1664))/(32)`

`t=(55 \pm √(1361))/(32)`

`t=(55 \pm 36.89)/(32)`

`t=(55 + 36.89)/(32) \ or \ t=(55- 36.89)/(32)`

`t=(91.89)/(32) \ or \ t=(18.11)/(32)`

`t=2.9 \ or \ t=0.6`

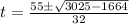
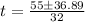
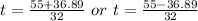
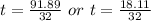
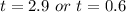
The value of t is t = 0.6 because this denotes the time taken by the ball to reach a height of 30 feet from the ground.

Therefore, the time taken by the ball to reach a height of 30 feet above the ground is 0.6 seconds.