Question

Can a triangle be drawn with a side length of three inches with angles at each end measuring 90 degrees and 89 degrees?

Answer 1

If the triangle has the angle of 90°, 89° and 1° then 1 side length can be 3 in but all the side lengths cannot be 3 in.

Step-by-step explanation:

The sum of all the angles of a triangle = 180°

So, if 1 angle is 90° and the 2nd angle is 89°, then the third angle will be 1°

and length of 1 side = 3 in

a = 3 in

Using the Sine rule,

`(sin A)/(a)= (sin B)/(b) = (sin C)/(c)`

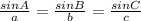
On substituting the value:

`(sin 90^o)/(3) = (sin 89^o)/(b) = (sin 1^o)/(c) \\\\(1)/(3) =(0.99)/(b)= (0.017)/(c) \\\\b = 3 X 0.99 = 2.97 in\\\\c = 3 X 0.017 = 0.051 in`

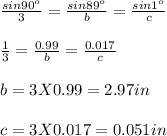
Therefore, if the triangle has the angle of 90°, 89° and 1° then 1 side length can be 3 in and the triangle will be very acute but all the side lengths cannot be 3 in.