Question

Which set of coordinates represents a function?

(0,5) (0,0) (1,1) (-2,4)
(1,10) (3,3) (1,2) (-1,1)
(2,15) (3,-3) (1,3) (0,0)
(3,20) (5,5) (1,4) (-1,-1)
(4,25) (5,-5) (1,5) (-2,-4)

Answer 1

Assuming that the domain is
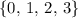`\lbrace0,\, 1,\, 2,\, 3\rbrace` (the set of whole numbers between 0 and 3, inclusive,) then only the third choice would represent a function:

`\lbrace{(2,\, 15),\, (3,\, -3),\, (1,\, 3),\, (0,\, 0)\rbrace}`.

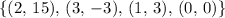Explanation:

A function needs to be

• one-to-one for all inputs in its domain, and
• defined for all values on its domain.

A map is one-to-one only if it maps each input to only one output.

For example, in
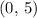`(0,\, 5)` in the first choice,
`0` is the input while
`5` is the output. If this set of coordinates is indeed one-to-one, then this input,

Similarly, the second set of coordinates tries to map the input
`1` to both
`10` and
`2`. This option isn't one-to-one and does not represent a function, either.

Indeed, the third, fourth, and fifth options are all one-to-one. However, there are gaps in the domain of the fourth and fifth option. (The domain of a map is the set of all the points in its definition.)

• The domain of the third option is
  `\lbrace0,\, 1,\, 2,\, 3\rbrace`.
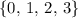• The domain of the fourth option is
  `\lbrace-1,\, 1,\, 3,\, 5\rbrace`.
• The domain of the fifth option is
  `\lbrace-2,\, 1,\, 4,\, 5\rbrace`.

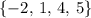Note, that whether these options are functions depend on the choice of the domain. For example, if the domain is merely
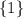`\lbrace1\rbrace`, then all three options would be functions. However, if the domain is the set of all integers (
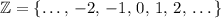`\mathbb{Z}= \lbrace\dots,\, -2,\, -1,\, 0,\, 1,\, 2,\, \dots\rbrace`,) then none of these choices will be a function.