Answer:
The sum of the two vectors is the vector <-0.5 , 4+3.5
 >
>
Explanation:
The horizontal component (x) of a vector whose magnitude is b units and its direction is Ф° is b cos Ф
The vertical component (y) of a vector whose magnitude is b and its direction is Ф is b sin Ф
The vector is <b cos Ф , b sin Ф>
∵ The vector goes 7 units at an angle
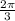
- That means its magnitude is 7 and its direction is
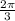
∴ x = 7 cos(
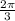 )
)
∴ y = 7 sin(
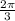 )
)
∵ cos(
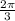 ) =
) =
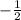
∵ sin(
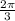 ) =
) =
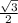
- Substitute them in x and y
∴ x = (7)(
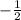 )
)
∴ x = -3.5
∴ y = (7)(
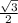 )
)
∴ y = 3.5

∴ The vector is <-3.5 , 3.5
 >
>
Now lets add the vectors by adding xs and ys components
∵ <3 , 4> + <-3.5 , 3.5
 > = <3 + -3.5 , 4 + 3.5
> = <3 + -3.5 , 4 + 3.5
 >
>
∴ <3 , 4> + <-3.5 , 3.5
 > = <-0.5 , 4+3.5
> = <-0.5 , 4+3.5
 >
>
∴ The sum of the two vectors is the vector <-0.5 , 4+3.5
 >
>