Question

The graph of the function f(x)=(x-4)(x+1) is shown below. which statement about the function is true?

(1) the function is increasing for all real values of X where X < 0

(2) the function is increasing for all real numbers of x where X < -1 and x>4

(3) the function is decreasing for all real numbers of x where x< 1.5

Answer 1

(3) the function is decreasing for all real numbers of x where x< 1.5

Explanation:

The function given in this problem is

`f(x)=(x-4)(x+1)`

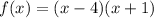
which can be rewritten as:

`f(x)=x^2-4x+x-4=x^2-3x-4`

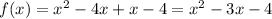
A function is:

- Increasing over a certain interval if the first derivative
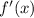`f'(x)` is positive in that interval

- Decreasing over a certain interval is the first derivative
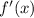`f'(x)` is negative in that interval

So we start by calculating the first derivative of this function. We get:

`f'(x)=2x^(2-1)-3x^(1-1)=2x-3`

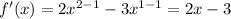
This function is positive when:

`2x-3>0\\2x>3\\x>(3)/(2)`

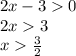
Which means, when x > 1.5.

So the function is:

- Increasing for x > 1.5

- Decreasing for x < 1.5

So the correct option is

(3) the function is decreasing for all real numbers of x where x< 1.5