Question

Find the value of x and the value of y

Answer 1

A

Explanation:

Since DE is parallel to AB and intersects the other 2 sides, it divides those sides proportionally, that is

`(BE)/(EC)` =
`(AD)/(DC)`

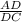
Note that AD = 33 - 22 = 11

Substitute values into the ratio

`(x)/(16)` =
`(11)/(22)` =
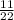`(1)/(2)` ( cross- multiply )

2x = 16 ( divide both sides by 2 )

x = 8

To find y use similar triangles

Δ ABC is similar to Δ DEC, thus ratios of corresponding sides are equal

`(AB)/(DE)` =
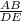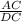`(AC)/(DC)`, substitute values

`(18)/(y)` =
`(33)/(22)` =
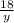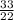`(3)/(2)` ( cross- multiply )

3y = 36 ( divide both sides by 3 )

y = 12

Thus y = 12, x = 8 → A

Answer 2

y = 15.1 , x = 11.7

Explanation:

Using pythagoras theorem

Hypothenus ^2 = opposite^2+adjacent ^2

33^2= 18^2+(16+Using pythagoras theorem

Hypothenus ^2 = opposite^2+adjacent ^2

22^2= 16^2+y^2

484= 256+y^2

484-256 = y^2 = 228

y = sqrt 228 = 15.0996688705= 15.1

Using pythagoras theorem

Hypothenus ^2 = opposite^2+adjacent ^2

33^2= 18^2+(16+x)^2

1089= 324+(16+x)^2

1089-324= (16+x)^2

765 = (16+x)^2

16 + x = sqrt 765

16 + x = 27.6586333719

x = 27.6586333719 -16 = 11.6586333719 = 11.7