Question

Consider the functions:

ƒ(x) = 0.25x + 25 and g(x) = 15(1.25)x

As x approaches ∞, which statement is correct?
A) The linear function will always exceed the exponential function.
B) The exponential function will always exceed the linear function.
C) The linear function will exceed the exponential function since its initial value is greater.
D) The exponential function will exceed the linear function since its base is greater than one.

Answer 1

As x approaches infinity, the exponential function g(x) = 15(1.25)^x will exceed the linear function f(x) = 0.25x + 25 due to the nature of exponential growth.

Step-by-step explanation:

When considering the functions f(x) = 0.25x + 25 and g(x) = 15(1.25)^x as x approaches ∞ (infinity), it is important to understand the nature of linear and exponential functions.

The linear function, f(x), grows at a constant rate, shown by its constant slope of 0.25. In comparison, the exponential function, g(x), grows at a rate that increases with x, since the base, 1.25, is greater than one. Therefore, as x approaches infinity, the exponential function will always exceed the linear function. This is due to the exponential growth rate becoming increasingly rapid compared to the steady increase of the linear function.

The correct answer to the question is B) The exponential function will always exceed the linear function.

Answer 2

Correct option D) Base of exponential function
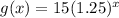`g(x) = 15(1.25)^x` is greater than 1 , this function will exceed linear function
`f(x) = 0.25x + 25` .

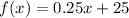Step-by-step explanation:

Here we have , f(x) = 0.25x + 25 and g(x) = 15(1.25)x . We need to tell As x approaches ∞, which function exceeds whom! Let's find out:

• f(x) = 0.25x + 25

This function is a linear function with an equation of straight line , having slope and y-intercept as :

`m=0.25\\c=25`

Graph for this function is attached below .

• g(x) = 15(1.25)^x

This function is an exponential function in the form of
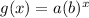`g(x) = a(b)^x` , where b>1 i.e. for rise in value of x there is exponential increase in value of y or , function .Basically Base of this exponential is greater than 1 , which makes it an increasing function ! Graph for this function is attached below .

Now , Comparing both graphs we see that as x approaches ∞ graph of exponential function
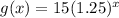`g(x) = 15(1.25)^x` is much more vertical than linear function
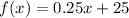`f(x) = 0.25x + 25` . Since , base of exponential function
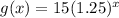`g(x) = 15(1.25)^x` is greater than 1 , this function will exceed linear function
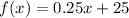`f(x) = 0.25x + 25` .Correct option D)