Question

The following colored pens were placed in a backpack.

• 3 red
. 3 black
• 2 blue
. ? purple
How many purple pens need to be in the backpack in
order for the probability of pulling out a red pen, no
replacing it, then pulling out a purple pen to be 1/15?​

Answer 1

The number of purple pen is 2

Step-by-step explanation:

Number of red pens = 3

Number of black pens = 3

Number of blue pens = 2

Number of purple pens = ?

Probability =
`(1)/(15)`

Total number of pens = 3 + 3 + 2 + x

= 8 + x

The probability of pulling out a red pen =
`(3)/(8+x)`

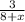
Total number of pens become = 8 + x - 1

= 7 + x

Probability of pulling out a purple pen =
`(x)/(7+x)`

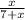
According to the question:

`(3)/(8+x) X(x)/(7+x) = (1)/(15)`

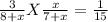
Solving the equation:

`(3x)/(8(7+x) + x (7+x)) = (1)/(15) \\\\(3x)/(56 + 8x + 7x + x^2) = (1)/(15) \\`

`(3x)/(56+ 15x + x^2) = (1)/(15) \\\\45x = 56 + 15x + x^2\\\\x^2 - 30x + 56 = 0\\\\x = 28, 2`

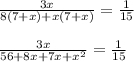
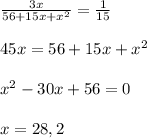
If x = 2 then,

`(3)/(8 +2) X (2)/(7+2) = (3)/(10) X (2)/(9) = (1)/(15)`

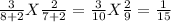
Therefore, the number of purple pen is 2