Question

Identify the properties used to perform the following simplifications:

Q1) log(100) = log(400) - log(4)
Q2) log(x^2) = log(x) + log(x)
Q3) log(49) = 2log(7)
Q4) Which properties would you use to simplify the following expression?
log (17x^3) two properties

Properties:
1. log(xy) = logx + logy

2. log(x/y) = logx − logy

3. log(x^r) = r logx

Answer 1

Answer: 2,1,3 welcome

Step-by-step explanation:

Answer 2

Property

Q1) log(100) = log(400) - log(4) ↔ 2.
`\log (x/y)=\log x - \log y`

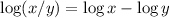
Q2) log(x²) = log(x) + log(x) ↔ 1.
`\log (xy)=\log x+\log y`

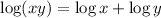
Q3) log(49) = 2log(7) ↔ 3.
`\log (x^r)=r\log x`

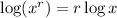
Q4) Which properties would you use to simplify the following expression? log (17x³):

• 1.
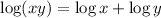  `\log (xy)=\log x+\log y`, and

• 3.
  `\log (x^r)=r\log x`

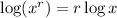
Step-by-step explanation:

Properties

1.
`\log (xy)=\log x+\log y`

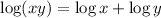
This property means that the logarithm of a product is equal to the sum of the logariths of the factors.

x² may be written as the product x · x

Then, the logarithm of x² is the same that the logarithm of x · x

And you can apply the rule of the logarithm of a product:

• log(x²) = log (x·x) = log(x) + log(x)

Hence, the property applied to Q2) is the number 1.

2.
`\log (x/y)=\log x - \log y`

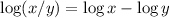
This property states that the logarithm of a quotient is equal to the logarithm of the dividend less the logarithm of the divisor.

The number 100 can be written as the quotion 400/4. Then:

• log(100) = log (400/4)

And, by the second property:

• log(400/4) = log(400) - log(4)

Thus, the property use to simplify the Q1) is the number 2.

3.
`\log (x^r)=r\log x`

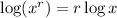
This property states that the logaritm of a power is equal to the exponent multiplied by the logarithm of the base

Then, since 49 = 7², you can write:

• log (49) = log (7²)

• log (7²) = 2 × log (7) = 2log(7)

Therefore, the property used to perform the simplification of Q3) is the third one.

Q4)

The given expression, log (17x³,) is the logarithm of a product: the product of 17 and x³.

Thus, you apply the property number 1:

• log (17x³) = log (17) + log(x³)

Now, you can simplify the second term: since x³ is a power you can use the property number 3, logarithm of a power, to find:

• log(x³) = 3log(x)

Then, the expression simplified is:

• log(17x³) = log(17) + 3log(3), for which you had to use two properties of the logarithms: number 1, and number 3.