Question

Check all that apply. If csc = 13/12, then:

Answer 1

Explanation:

I don't know where you are in your class, or even what chapter you are in, but I solved this using a right triangle.

We don't need to know the angles, just the sides.

c is the hypotenuse, the line at a tilt

b is the adjacent line, directly below c

a is the opposite line

c = 13

a= 12

b = ?

In order to find b, we use the Pythagorean Theorem,
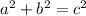`a^(2) + b^(2) = c^(2)`, but we need to rearrange the problem to where we are solving for b instead of c,
`b^(2) = a^(2) + c^(2)`

`b^(2) = (12)^(2) + (13)^(2)\\b^(2) = 144 + 169\\b^(2) = 313 \\\sqrt{b^(2) } = √(313)\\ b = 17.69`

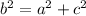
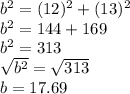
So, b = 17.69

Now, we need to evaluate each of the trig. functions:

`sin = (opposite)/(hypotenuse) = (12)/(13) \\csc = (hypotenuse)/(opposite) = (13)/(12) \\cos = (adjacent)/(hypotenuse) = (17.69)/(13) \\sec = (hypotenuse)/(adjacent) = (13)/(17.69)\\tan = (opposite)/(adjacent) = (12)/(17.69)\\cot = (adjacent)/(opposite) = (17.69)/(12)`

So, there is your answers, hope that is what you are looking for.