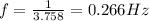Answer:
1)
The period of a simple pendulum is given by the formula:
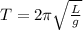
where
L is the length of the pendulum
g is the acceleration due to gravity
In this problem we have:
L = 3.50 m is the length of the pendulum
At the North Pole, we have
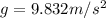
So the period is
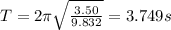
At Chicago, we have
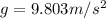
So the period is
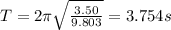
At Jakarta, we have
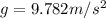
So the period is
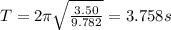
2)
The frequency of an object in simple harmonic motion is equal to the reciprocal of the period:
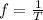
At the North Pole, we have
T = 3.749 s
So the frequency is
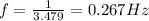
At Chicago, we have
T = 3.754 s
So the frequency is
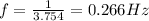
At Jakarta, we have
T = 3.758 s
So the frequency is