The probability that a grain of rice dropped onto the circles at random lands outside the circle with the 4-cm radius and inside the circle with a radius of 8 cm is
 or 75%.
or 75%.
Explanation:
Step 1:
First, we need to calculate the areas of both circles.
The area of a circle
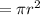 where r is the radius of the circle.
where r is the radius of the circle.
The inner-circle has a radius of 4 cm.
The area of the inner circle

The outer circle has an inner radius of 4 cm and an outer radius of 8 cm.
So its area is
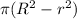 where R is the outer radius and r is the inner radius.
where R is the outer radius and r is the inner radius.
The area of the outer circle
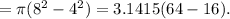
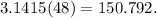
So the inner circle has an area of 50.264 square cm and the outer circle has an area of 150.792 square cm.
Step 2:
To find the probability of an event we divide the number of favorable outcomes by the total number of outcomes.
The total number of outcomes is the area of the entire circle
 square cm.
square cm.
The number of favorable outcomes is the area of the outer circle i.e. 150.792 square cm.
The probability of the rice falling in the outer circle
 .
.