the probability of selecting a drama and then a comedy with replacement and without replacement is 4/49 and 2/21 respectively !
Explanation:
Here we have , Angel has seven DVD movies on a shelf: 4 dramas, 2 science fiction movies, and 1 comedy. Two movies will be selected at random. We need to Determine the probability of selecting a drama and then a comedy with replacement and without replacement. Let's find out:
With replacement :
Probability of selecting a Drama movie :
⇒

Probability of selecting comedy movie :
⇒

Probability for both events is :
⇒
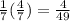
Without replacement :
Probability of selecting a Drama movie :
⇒

Probability of selecting comedy movie :
⇒

Probability for both events is :
⇒
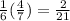
Therefore , the probability of selecting a drama and then a comedy with replacement and without replacement is 4/49 and 2/21 respectively !