Answer:
- Sum of first 150 positive even integers is 22650
Explanation:
We know that first 150 postive even Integers are 2,4,6,8,10... 300.
Here,
- First term (a) = 2
- Comman difference (d) = 4 - 2 = 2
- Total terms (n) = 150
- Last term (aₙ) = 300

Substituting values in the formula:


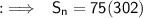
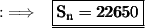
- Sum of first 150 positive even integers is 22650