Question

Find the sum of the first 150 positive even integers.

Answer 1

• Sum of first 150 positive even integers is 22650

Explanation:

We know that first 150 postive even Integers are 2,4,6,8,10... 300.

Here,

• First term (a) = 2
• Comman difference (d) = 4 - 2 = 2
• Total terms (n) = 150
• Last term (aₙ) = 300

`\\`

Substituting values in the formula:

`\\ :\implies \sf \: \: S_(n) = (n)/(2) (a + a_(n)) \\ \\`

`:\implies \sf \: \: S_(n) = (150)/(2) (2 + 300) \\ \\`

`:\implies \sf \: \: S_(n) = 75(302) \\ \\`

`:\implies \: \:{ \underline{ \boxed{ \pmb{ \pink { \rm{S_(n) = 22650 }}}}}} \\ \\`

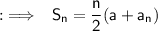
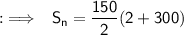
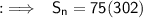
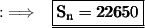
• Sum of first 150 positive even integers is 22650

Answer 2

• The number series 2, 4, 6 , 8. . . . , 150.
• The first term (a) = 1
• The common difference (d) = 4 – 2 = 2
• Total number of terms (n) = 150
• last term (an) = 300

Formula for finding sum of nth terms =

n/2 × (a + an)

putting the known values ,

Sum = 150/2 × ( 2+300)

Sum = 75 × 302

Sum of first 150 positive even integers = 22650