1 Answer

Louie Miranda · Answer 1 · 2021-01-15T08:35:38+0000

a. In order for
to be a proper density function, its integral over its domain must evaluate to 1:

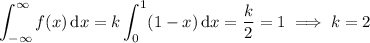
$\displaystyle\int_(-\infty)^\infty f(x)\,\mathrm dx=k\int_0^1(1-x)\,\mathrm dx=\frac k2=1\implies k=2$

also must be non-negative over its support, which is the case here.

I assume the instruction regarding the distribution function doesn't apply to parts (b) and (c).

(b) Integrate the density over the interval [0.1, 0.2]:

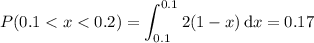
$P(0.1<x<0.2)=\displaystyle\int_(0.1)^(0.1)2(1-x)\,\mathrm dx=0.17$

(c) Integrate the density over the interval [0.5, 1]:

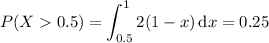
$P(X>0.5)=\displaystyle\int_(0.5)^12(1-x)\,\mathrm dx=0.25$

The distribution function is obtained by integrating the density:

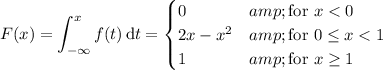
$F(x)=\displaystyle\int_(-\infty)^xf(t)\,\mathrm dt=\begin{cases}0&\text{for }x<0\\2x-x^2&\text{for }0\le x<1\\1&\text{for }x\ge1\end{cases}$

(d) Using the distribution function, we have

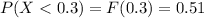
P(X<0.3)=F(0.3)=0.51

(e) Using
again, we get

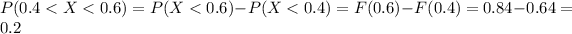
P(0.4<X<0.6)=P(X<0.6)-P(X<0.4)=F(0.6)-F(0.4)=0.84-0.64=0.2

(f) The mean is

$E[X]=\displaystyle\int_(-\infty)^\infty x\,f(x)\,\mathrm dx=\int_0^12x(1-x)\,\mathrm dx=\frac13$

The variance is

V[X]=E[(X-E[X])^2]=E[X^2]-E[X]^2

where

$E[X^2]=\displaystyle\int_(-\infty)^\infty x^2\,f(x)\,\mathrm dx=\int_0^12x^2(1-x)\,\mathrm dx=\frac16$

so that the variance is

$V[X]=\frac16-\left(\frac13\right)^2=\frac1{18}$

Please log in or register to add a comment.