Question

A circle is shown. Secants S V and T V intersect at point V outside of the circle. Secant S V intersects the circle at point W. Secant T V intersects the circle at point U. The length of T U is y minus 2, the length of U V is 8, the length of S W is y +4, and the length of W V is 6. What is the length of line segment SV? 6 units 8 units 12 units 16 units

Answer 1

16

Explanation:

16

Answer 2

Given:

Secants S V and T V intersect at point V outside of the circle. Secant S V intersects the circle at point W. Secant T V intersects the circle at point U.

The length of TU is (y - 2).

The length of UV is 8.

The length of SW is (y + 4)

The length of WV is 6.

We need to determine the length of line segment SV.

Value of y:

The value of y can be determined using the intersecting secant theorem.

Applying, the theorem, we get;

`WV * SV=UV * TV`

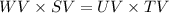
Substituting the values, we have;

`6 * (y+4+6)=8 * (y-2+8)`

`6 * (y+10)=8 * (y+6)`

`6y+60=8y+48`

`-2y+60=48`

`-2y=-12`

`y=6`

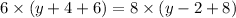
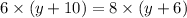
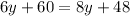
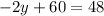
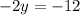
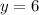
Thus, the value of y is 6.

Length of SV:

The length of SV is given by

`SV=SW+WV`

`SV=y+4+6`

`SV=6+4+6`

`SV=16`

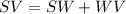
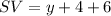
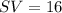
Thus, the length of SV is 16 units.

Hence, Option D is the correct answer.