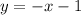Answer:
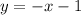
Explanation:
The Slope-Intercept form of the equation of the line is:

Where "m" is the slope and "b" is the y-intercept.
When you have a System of Linear equations and the lines are exactly the same line, you can identify that the System has Infinitely many solutions.
In this case, you know that the Line M is represented by the following equation:

Solving for "y" , you get:
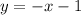
You can identify that:

Therefore, to the set of equations has infinitely many solutions, the Line M and the Line P must be exactly the same.
Then, you can determine that the Line P is represented by the following equation: