Question

A teacher writes the following product on the board: \qquad (3x^2)(4x) = 12x^3(3x 2 )(4x)=12x 3 left parenthesis, 3, x, squared, right parenthesis, left parenthesis, 4, x, right parenthesis, equals, 12, x, cubed Miles concludes that 3x^23x 2 3, x, squared is a factor of 12x^312x 3 12, x, cubed. Jude concludes that 12x^312x 3 12, x, cubed is divisible by 4x4x4, x.

Answer 1

4x4x4x45x5x6x67

Explanation:

keireww

Answer 2

Both students are right.

Explanation:

The product that the teacher wrote on the board is

`\qquad (3x^2)(4x) = 12x^3`

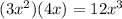
One of his students called Miles, conclude that

`3 {x}^(2)`

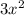
is a factor of

`12 {x}^(3)`

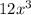
This is very true because from the given product both 3x² and 4x are factors of 12x³.

Another student , Jude also concludes that 12x³ is divsible by 4x.

This is also true because:

`\frac{12 {x}^(3) }{4x} = 3 {x}^(2)`

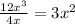
Hence both students are correct.