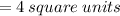Question

What is J|X-2|dx (from 0 to 4). Drawing a picture of the V-shaped graph which touches

the x-axis at 2 helps. Geometry, not calculus.
a. O b. 1. c. 2 d. 4



I am having trouble trying to solve this problem can anyone help?

Answer 1

d. 4

Explanation:

We want to evaluate

`\int _(0) ^(4) |x - 2| dx`

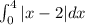
geometrically.

The graph of

`y = |x - 2|`

is a V-shaped graph with vertex at (2,0).

Geometrically, we want to find the area under this curve from x=0 to x=4.

This V-shaped graph formed two congruent triangles as shown in attachment.

The area of the triangle with height 2 units and base 2 units is

`= (1)/(2) bh`

`= (1)/(2) * 2 * 2`

`= 2 \: square \: units`

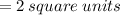
Since the triangles are two we multiply by 2 to get:

`= 4 \: square \: units`