Question

Show all of your work, even though the question may not explicitly remind you to do so. Clearly label any functions, graphs, tables, or other objects that you use. Justifications require that you give mathematical reasons, and that you verify the needed conditions under which relevant theorems, properties, definitions, or tests are applied. Your work will be scored on the correctness and completeness of your methods as well as your answers. Answers without supporting work will usually not receive credit.

Unless otherwise specified, answers (numeric or algebraic) need not be simplified. If your answer is given as a decimal approximation, it should be correct to three places after the decimal point.

Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.

A particle moves along the l-axis so that its position at time t>0 is given by x(t) = (t^2 - 9)/(3t^2 + 8)

(a) Is the particle moving toward the origin or away from the origin at time t = 2 ?
(b) The acceleration of the particle is given by a (t). Write an expression for a (t), and find the Value of a(2)
(c) what position does the particle approach as(t) approaches infinity?

Answer 1

(a) at t=2, the particle is moving toward the origin

(b) a(t) = 70(8 -9t^2)/(3t^2 +8)^3; a(2) = -0.245

(c) the particle approaches x = 1/3 as t gets large

Explanation:

(a) The function x(t) is negative for -3 < t < 3, so at t = 2, the particle is to the left of the origin.

The velocity of the particle is given by the derivative of the position function:

`x'(t)=((3t^2+8)(2t)-(t^2-9)(6t))/((3t^2+8)^2)=(70t)/((3t^2+8)^2)`

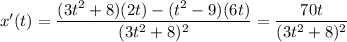
Then, at t=2, the expression is positive, indicating the particle is moving toward the origin.

__

(b) The acceleration is the derivative of the velocity, so is ...

`a(t)=(70(3t^2+8)^2-(70t)(12t)(3t^2+8))/((3t^2+8)^4)=(70(3t^2+8-12t^2))/((3t^2+8)^3)\\\\\boxed{a(t)=(70(8-9t^2))/((3t^2+8)^3)}`

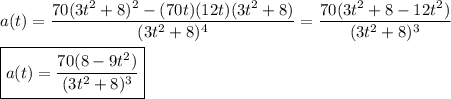
Then at t=2, the acceleration is ...

a(2) = 70(8 -9·4)/(3·4+8)^3 = 70(-28)/8000

a(2) = -0.245

__

(c) As t gets large, the value of x(t) approaches t^2/(3t^2) = 1/3.