Question

An oil drop with a charge of 2x10-17C is suspended between 2 parallel plates 5cm apart. The

potential difference between the plates is 10kV. Calculate the mass of the oil drop and the
number of excess electrons it is carrying.​

Answer 1

1) Mass:
`4.1\cdot 10^(-13)kg`

2) Electrons: 125

Step-by-step explanation:

1)

The electric force exerted on the oild drop is given by

`F=qE`

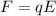
where

q is the charge on the oil drop

E is the magnitude of the electric field

The electric field between two parallel plates can be written as

`E=(V)/(d)`

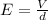
where

V is the potential difference

d is the separation between the plates

So the electric force is

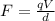`F=(qV)/(d)` (1)

On the other hand, the gravitational force on the oil drop is

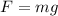`F=mg` (2)

where

m is the mass of the drop

g is the acceleration due to gravity

The two forces have opposite directions (electric force: upward, gravity: downward), so the oil drop remains in equilibrium if the two forces have same magnitude. So,

`(qV)/(d)=mg`

Here we have

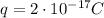`q=2\cdot 10^(-17)C` is the charge of the oil drop

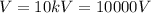`V=10 kV=10000 V` is the potential difference

`d=5 cm = 0.05 m` is the separation between the plates

`g=9.8 m/s^2` is the acceleration due to gravity

Solving for m, we find the mass of the oil drop:

`m=(qV)/(dg)=((2\cdot 10^(-17))(10000))/((0.05)(9.8))=4.1\cdot 10^(-13)kg`

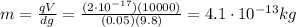
2)

From the text of the problem, we know that the net charge on the oil drop is

`Q=-2\cdot 10^(-17)C`

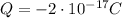
Where the charge is negative since it is due to an excess of electrons (which are negatively charged).

The net charge on the oil drop can be written as

`Q=Ne`

where

N is the number of excess electrons

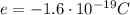`e=-1.6\cdot 10^(-19)C` is the charge on one electron (the fundamental charge)

Therefore, here we can solve the formula for N, to find the number of excess electrons on the oil drop:

`N=(Q)/(e)=(-2\cdot 10^(-17))/(-1.6\cdot 10^(-19))=125`

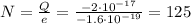
So, 125 excess electrons.