Answer:
The height of triangle OAB is 8 cm
Explanation:
The question in English is
Find the length of the height of the triangle OAB dropped to the side of AB, if the perimeter of the triangle OHV is 24 cm, and the diameter of the circle shown is 20 cm, AB = 12 cm.
The picture of the question in the attached figure
we know that
If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc
In this problem the diameter of the circle CD is perpendicular to the chord AB, that means that the diameter bisect the chord
so
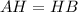
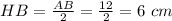
Remember that the perimeter of triangle is equal to the sum of its three length sides
so
Perimeter of triangle OHB is given by
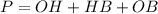
we have
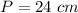
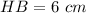
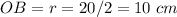 ---> the radius is half the diameter
---> the radius is half the diameter
substitute the given values
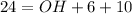
solve for OH
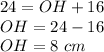
therefore
The height of triangle OAB is 8 cm