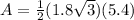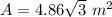Question

Muriel plans to make a sail in the shape of a right triangle for her boat. She wants the largest part of the sail to make a 60- degree angle with the horizontal . How many square meters of material will she need to make the sail?

Answer 1

`A=4.86√(3)\ m^2`

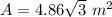
Explanation:

The complete question in the attached figure

we know that

The area of triangle is given by the formula

`A=(1)/(2)(b)(h)`

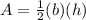
we have

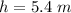`h=5.4\ m` ----> given problem

Find the value of b

In the right triangle of the figure (a sail)

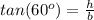`tan(60^o)=(h)/(b)` ---> by TOA (opposite side divided by the adjacent side)

we have

`tan(60^o)=√(3)`

`h=5.4\ m`

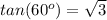
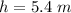
substitute

`√(3)=(5.4)/(b)`

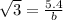
solve for b

`b=(5.4)/(√(3))=1.8√(3)\ m`

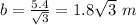
Find the area

`A=(1)/(2)(1.8√(3))(5.4)`

`A=4.86√(3)\ m^2`