Question

Given that 0≤β<2π, which of the following gives all solutions to the equation 2sin2β=9sinβ−4?

Answer 1

`\beta=0.728 \\ \\ \beta=2.824`

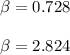
Step-by-step explanation:

We know the following equation:

`2sin2\beta=9sin\beta-4 \\ \\ \text{We can write this as follows:} \\ \\ \\ Subtract \ 9sin\beta \ from \ boths \ sides: \\ \\ 2sin2\beta-9sin\beta=9sin\beta-9sin\beta-4 \\ \\ 2sin2\beta-9sin\beta=-4 \\ \\ \\ Add\ 4 \ to \ boths \ sides: \\ \\ 2sin2\beta-9sin\beta+4=-4+4 \\ \\ 2sin2\beta-9sin\beta+4=0`

So we can write this equation as two function that are equalized, that is:

`f(\beta)=2sin2\beta-9sin\beta+4 \\ \\ g(\beta)=0 \\ \\ \\ So: \\ \\ f(\beta)=g(\beta)`

So let's solve this equation graphically. We know that:

`0\leq \beta<2\pi`

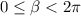
And this interval is indicated with the two vertical lines drawn in red below. For this graph the x-axis represents β.

So the β-values of the graph of f(β) that makes this function to be zero are:

`\beta=0.728 \\ \\ \beta=2.824`

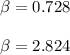
And those two values lies on the given interval.