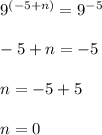Answer:
Step-by-step explanation:
The expressions are garbled. The correct expressions to determine the product of powers are:
1. What is the value of x in the product of powers
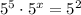 ?
?
2. What is the value of y in the product of
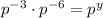 ?
?
3. What is the value of n in th product of
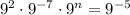 ?
?
Solutions
1. What is the value of x in the product of powers
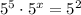 ?
?
Apply the rule of the product of powers with the same base to the left side of the equality.
The product of two powers with the same base is the base raised to the sum of the exponent:
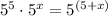
Now the power on the left side has the same base as the power on the right side, so the exponents are the same:
2. What is the value of y in the product of
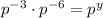 ?
?
Again, the product of the two powers on the left side is equal to the common base raised to the sum of the exponents:
On the left side, you get:

Then,
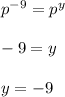
3. What is the value of n in th product of
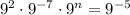 ?
?
Same rule:
Left side:
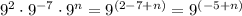
Left side equal to right side: