1 Answer

Ali Turki · Answer 1 · 2021-09-15T14:06:24+0000

Given:

The radius of the figure is 5 mm

The height of the cylinder is 9 mm.

Volume of the composite figure is made of two half spheres and a cylinder.

We need to determine the volume of the composite figure.

Volume of a cylinder:

Volume of a cylinder is given by

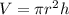
$V=\pi r^2h$

Substituting r= 5, h = 9, we get;

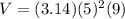
V=(3.14) (5)^2(9)

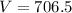
V=706.5

Thus, the volume of the cylinder is 706.5 mm³

Volume of the hemisphere:

Volume of the hemisphere is given by

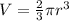
$V=(2)/(3) \pi r^3$

Substituting r = 5, we get;

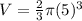
$V=(2)/(3) \pi (5)^3$

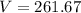
V=261.67

Thus, the volume of the hemisphere is 261.67 mm³

Volume of the composite figure:

The volume of the composite figure can be determined by adding the volume of the cylinder and 2 hemispheres.

Thus, we have;

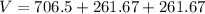
V= 706.5+261.67+261.67

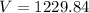
V=1229.84

Thus, the volume of the composite figure is 1229.84 mm³

Please log in or register to add a comment.